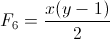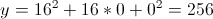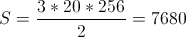Introduction about the Geodesic Dome

In this part, we'll talk about the Biosphere, in Montreal (Canada).
The Biosphere is a geodesic dome which contains a museum about environment.
We have no doubt you're wondering : where is the relation between a geodesic dome, mathematics and the harmony of architectures ? We're going to explain it to you, demonstrating the link between mathematics and a geodesic dome, and after showing that a geodesic dome can be harmonious.

We'll follow this plan :

1. Parameters of a geodesic dome
2. How to build a geodesic dome ? And what is finally a geodesic dome ?
3. The second shape of a geodesic dome
4. Calculations and properties in a geodesic dome
5. Geodesic dome and harmony

The three first steps will explain the "rules" of the construction of the geodesic dome, whereas the fourth is about calculations and the last is a kind of conclusion with a link with harmony.

So, let's go !

.

Parameters of a Geodesic Dome

 So, we're going to begin with the construction of a geodesic dome. For that, you have to know and understand the three parameters of a geodesic dome. This parameters were discovered by Richard Buckminster Fuller during his experiences in 1948-1949. He also showed that geodesic domes are ideal for gorgeous architectures.

The first parameter is the number of faces which have a vertex in common, called N.
 For example, in a tetrahedron N is equal to three, in an octahedron to four and in an icosahedron to five.

 Tetrahedron (N = 3)

Octahedron (N = 4)

Icosahedron (N = 5)

 A step in the construction of a geodesic dome consists of the separation of each side of a triangle in equal segments. If we take the triangle with a vertex at the top, we rely it with a point of the opposite side which have a equal segments on its left and b equal segments on its right. b is greater or equal to 0. a is greater than 0 and greater or equal to b.

a and b are the two other parameters of a geodesic dome and a+b is called frequency.

Example :  a = 3 and b = 2

Note :

• When b = 0, the geodesic dome belongs to class I and is called "triacon". 
• When a = b, the geodesic dome belongs to class II and is called "alternate". 
• The other cases belongs to class III. 

In the Biosphere, N = 5, a = 16 and b = 0. It belongs to the "triacon" class.

                                       

How to Make a Geodesic Dome

The Biosphere is a reinforced geodesic dome : it contains a "first layer" which is a normal geodesic dome and a "second layer" which is a dual geodesic dome. The two layers allow the geodesic dome to be more robust.

Here you'll learn how to make a geodesic dome, with the example of the Biosphere.

•  Step 1 : We begin with a polyhedron. There are three polyhedrons we can use : a tetrahedron, an octahedron or an icosahedron, which correspond to the variable N as you can see here. Most of the time, we build a geodesic dome with an icosahedron (N = 5). It's true in our example : the Biosphere. 

• Step 2 : Then, we cut every side in a + b equal segments (click here for more information a and b). In our case, a = 16 and b = 0. So, we link the vertex with the one which is at the right, in order to have 16 segments at the left.
  
  
  

• Step 3 : We do it again for the two other side. All triangles are equilateral (except some triangles on the edge of each side when the geodesic dome belongs not to the class I).

• Step 4 : We do steps 2 and 3 for all the other faces.
  
  
  

• Step 5 : We build the circumscribed sphere on the polyhedron, and we name the center O. We created the vertices of the geodesic dome, which are the intersection points between the sphere and lines passing by O and vertices of "little triangles" created in step 4. The new points are rely if and only if they come from vertices belong to the same triangle created in the step 4.
  
  
  
  
  
  

• Step 6 : We delete the lines of construction : the geodesic dome is now finished !
  
  
  

An other shape : the Duale

There is an other form of geodesic dome, called dual geodesic dome. This is the "second layer" of the Biosphere.

Its construction is the same as the regular geodesic dome, there is just an added step between the fifth and the sixth steps.

Then we have to determine on the sphere the centre of each spherical triangle.
For that, we trace the centreline of two sides of a triangle and repeat this step for all triangles.
If these points belong to adjacent faces of the regular geodesic dome, you have to join them two by two, creating the sides of the dual geodesic dome.
All these sides draw polygons :  these are the faces of the dual geodesic dome.
These faces are hexagons, except for twelve of them which are regular pentagons placed in front of the twelve vertices of the polyhedron used at the beginning.
Then, we apply the sixth step, deleting the construction lines, and we have finished.

Now it's your turn ! Create your own geodesic dome with this software.

To access it, click this link.

Calculations and Properties of a Geodesic Dome

Here, you're going to learn some calculations and properties related to geodesic domes. For example, in a small time, you'll be able to calculate the number of faces, vertices ans sides of any geodesic dome. However, you must know the three parameters of a geodesic dome : N, a and b (here are definitions of parameters).

You also have to know if the geodesic dome is a normal or a dual geodesic dome, because calculations are different (click if you don't remind what's a regular or a dual geodesic dome).

I Calculations 

We'll call F the number of faces, V the number of vertices and S the number of sides. First, we must calculate 2 other variables, which we called x and y. The calculations of x and y are :

In a regular geodesic dome :
The calculations of S, V and F are :

A regular geodesic dome has two types of vertices : many vertices are vertices of 6 faces at the same time (called V6), but some others are vertices of N faces (called VN). the calculations of V6 and VN are :

In a dual geodesic dome :
Here are the calculations of F, S and V :

A dual geodesic dome has two types of faces : many faces have 6 sides (called F6, these are hexagons), but some others have N sides (called FN, so triangles when N=3, squares when N=4 and pentagons when N=5). The calculations of F6 and FN are :

You can see formulas are identical in a regular or in a dual geodesic dome, but what you calculate is different (for example, we have the same calculations between the number of faces in a regular geodesic dome and the number of vertices in the dual geodesic dome). Don't forget that the construction of a dual geodesic dome is very close to that of the regular !

II Properties

Here are properties of 3 particular geodesic domes :

• If a=1 and b=0, the geodesic dome is the beginning solid. In fact, you cut all sides in a+b=1, so the solid remains the same.
• We can think that faces of geodesic domes are equilateral triangles, but it's wrong, except when a=b=1.
• If a=b or b=0, the geodesic dome has the same properties as its beginning polyhedron. For example, it has 15 planes of symmetry which cross 2 opposite sides. Otherwise, it doesn't have any plane of symmetry.

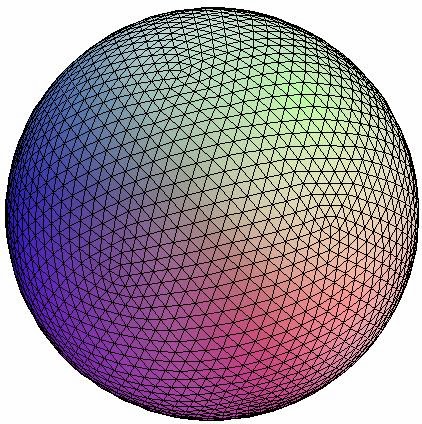
III Application in the Biosphere

As the Biosphere is a geodesic dome, we can use these calculations.
As you know, the three parameters (N, a and b) equal 5, 16 and 0 in the Biosphere. Moreover, these are "two" geodesic domes in the Biosphere, the normal and the dual. So, we're going to make all these calculations. Our calculations will be made as if the geodesic dome is "complete".

First, we must calculate x and y. So :

The normal geodesic dome :
The most visible geodesic dome in the Biosphere is the "normal", so we'll begin with this one.

I agree that it seems too big ! You probably think that it's not possible, but I answer that we can't imagine just looking at the Biosphere the number of faces. Our eyes easily deceive us !

2550 + 12 = 2562, so we find the total number of vertices : it's correct.

The dual geodesic dome :

As I said before, the results are the same, but not for the same thing.

Then, you can see that mathematics are once again omnipresent in architecture : here, in an architecture like the geodesic dome and the Biosphere, the area of algebra dominates too.