The Golden Triangle

The Pentagon :

One of the best-known construction in the US is the Pentagon, which is the United States Department of Defence (located in Virginia). Built in 1943, its architect is Georges Bergstrom. With its 5 floors and 28 km of corridors, the Pentagon is the largest office block in the world. It was of course built from a pentagon : it's a polygon with 5 equal sides.

But where is the golden number ?

Pentagons and Golden triangles

First, you must find that all we're going to do use regular pentagons, that means pentagons with 5 equal segments.
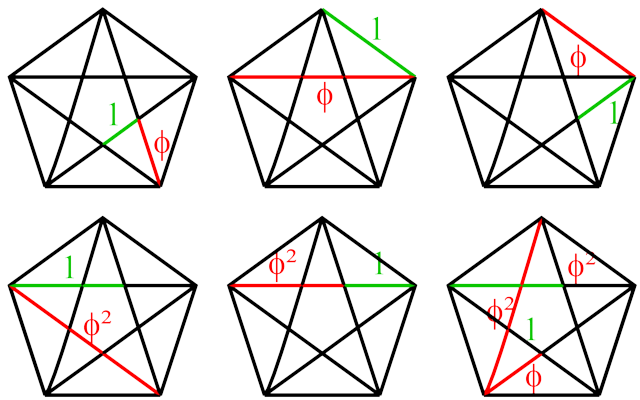
A pentagon can be made with a star with five branches, where each summit of the branches is linked with the one near it. This star is called a pentagram. In Antiquity, the pentagram was considered like the universal symbol of perfection. We can find the golden number in it :

Naturally, all is a story of proportionality.

In fact, when we find the golden number in the pentagon, we find golden triangles. But, what are golden triangles ?

A golden triangle is an isosceles triangle such as the ratio of a side a over an other side b which is different of a is  :

Here is the method to build a golden triangle :
First, you have to take a system (O, OB, OA ).

 Next, you have to trace the circular arch, length [AI], center I, which cuts the abscissa axis. The point of intersection is C. Take the length [OC] and report it in A, to place the point J and S1, like in the picture below. It makes your first isosceles triangle, which is a golden triangle.

 There are two "types" of golden triangles, which are define by their angles : they measure respectively 36° or 108° at the summit, and 72° or 36° at the base.

How to make a pentagon ?

Now, we're going to take an example of pentagon to prove you that it possess the golden number.
The golden triangle traced before
Trace the circle of center O and radius [OA], which will be the circumscribed circle of the pentagon. After, trace the parallel of the abscissa axis passing by S1. Thus, you find S5, which is the intersection point with the circle. After, you have to trace the line passing by S5 and J : the intersection point with the circle is S2. You do it again with S1, in order to find S4. S3 is just the intersection point between the circle and [AO].

If you want to have a pentagram, you just have to trace the diagonals :

 The small pentagon is regular too :  all sides are equal.

Where can we find the golden number ?
There are many ratios whose the result is a power of the golden number (power -1, 1 or 2). In fact, when the result is phi squared (2.61), you can find the inverse of phi (0.61) switching the numerator and the denominator of the initial fraction.
The ratios made come from golden triangles. For example, in the three first cases, we have the golden triangles LKS2, S1S2S5 and KS1S2.

LK / KS2 ≈ 1,61...
S1 S5 / S2 S5 ≈ 1,62...
K S2 /  S1 S2 ≈ 1,61...
S2 S5 / M S2 ≈ 2,61...
J S2 / K S2 ≈ 2,61...

1,61 is an approximate value for the golden number, and 2,61 is an approximate value of phi squared.
It does not always give the same values, because values on the picture are not exact. 
You must now that we find also golden triangles in decagons.